Функционирование системы ЗИ можно представить как процесс перехода из одного состояния в другое под воздействием каких-либо воздействий, приводящих к возникновению недостатков и нарушений, которые в свою очередь приводят к разглашению (утечке) сведений составляющих коммерческую тайну.
Таким образом система ЗИ в организации может быть представлена в виде системы S с накоплением недостатков и нарушений, которая в любой момент времени может находиться в одном из четырех состояний:
S1 – состояние, когда система функционирует без недостатков и нарушений;
S2 – состояние, когда система функционирует с недостатками и без нарушений;
S3 – состояние, когда система функционирует с нарушениями, накопление которых может привести к нарушению режима коммерческой тайны в организации;
S4 – состояние, когда система функционирует со значительными нарушениями, при водящих к нарушению режима коммерческой тайны в организации.
Таким образом функционирование системы ЗИ целесообразно представить с помощью графа состояний, вершины которой соответствуют состояниям системы ЗИ, а ребра – переходы из состояния в состояния. А так как существуют вероятности перехода из одного состояния в другое, то на графе состояний соответствующие вероятности перехода также могут быть отражены. В результате диаграмма состояний позволяет получить последовательность состояний системы защиты коммерческой тайны (рисунок 11).
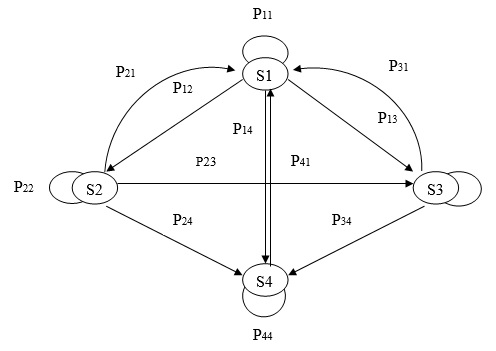
Рисунок 11. Граф состояний системы ЗИ
Таким образом система защиты коммерческой тайны представима в виде графа:
где U – множество вершин, определяющих возможные состояния системы ЗИ,
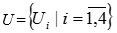
T – множество дуг, показывающих переходы из одного состояния в другое,
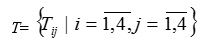
В данном случае дуги определяют следующие вероятностные переходы:
дуга T12 определяет с какой вероятностью P12 система ЗИ из состояния функционирования без недостатков и нарушений перейдет в состояние функционирования с недостатками и без нарушений; дуга T21 определяет с какой вероятностью P11 система ЗИ из состояния функционирования с недостатками и без нарушений перейдет в состояние функционирования без недостатков и нарушений; дуга T11 определяет с какой вероятностью P21 система ЗИ останется в состоянии функционирования без недостатков и нарушений; дуга T13 определяет с какой вероятностью P13 система ЗИ из состояния функционирования без недостатков и нарушений перейдет в состояние функционирования с нарушениями; дуга T31 определяет с какой вероятностью P31 система ЗИ из состояния функционирования с нарушениями перейдет в состояние функционирования без недостатков и нарушений; дуга T33 определяет с какой вероятностью P33 система ЗИ останется в состоянии функционирования нарушениями; дуга T23 определяет с какой вероятностью P23 система ЗИ из состояния функционирования с недостатками и без нарушений перейдет в состояние функционирования с нарушениями; дуга T24 определяет с какой вероятностью P24 система ЗИ из состояния функционирования с недостатками и без нарушений перейдет в состояние функционирования со значительными нарушениями; дуга T22 определяет с какой вероятностью P22 система ЗИ останется в состоянии функционирования с недостатками и без нарушений; дуга T14 определяет с какой вероятностью P14 система ЗИ из состояния функционирования без недостатков и нарушений перейдет в состояние функционирования со значительными нарушениями; дуга T44 определяет с какой вероятностью P44 система ЗИ останется в состоянии функционирования со значительными нарушениями; дуга T41 определяет с какой вероятностью P41 система ЗИ перейдет из состояния функционирования со значительными нарушениями в состояние функционирования без недостатков и нарушений; дуга T34 определяет с какой вероятностью P34 система ЗИ из состояния функционирования с нарушениями перейдет в состояние функционирования со значительными нарушениями.
Однако модель функционирования системы ЗИ в виде графа не позволяет учитывать динамику процесса функционирования системы ЗИ и проводить соответственно мероприятия по подготовке к проведению контроля.
Для проведения мероприятий по подготовке к проведению контроля, необходимо учесть динамику функционирования системы ЗИ. Для простоты изложения рассмотрим систему ЗИ в установившемся режиме. В данном случае наиболее предпочтительным математическим аппаратом для исследования функционирования системы ЗИ является теория Марковских цепей, которая позволяет определить с какой вероятностью будет находиться система СЗИ S после k-го шага.Таким образом основными характеристиками системы ЗИ являются вероятности нахождения ее в i-м состоянии Pi (k)=P(Si(k))(i=1,…, 4; k=1, n) k=1, n .
Вероятности Pi(k) (i=1,…4; k=1, n) называются вероятностями состояний.
Кроме того, вероятность i-го состояния на k шаге Pi (k) есть вероятность того, что система S от k до (k+1) шага будет пребывать в состоянии Si.
Переходные вероятности однородной цепи Pij образуют квадратную матрицу. Она обладает следующими свойствами:
каждая строка характеризует выбранное состояние системы, а ее элементы представляют собой вероятности всех возможных переходов за один шаг из выбранного состояния, в том числе и переход в саму себя;
элементы столбцов показывают вероятности всех возможных состояний системы за один шаг в заданное время;
сумма вероятностей каждой строки равна единицы, так как переходы образуют полную группу несовместимых событий:
по главной диагонали матрицы переходных вероятностей стоят вероятности Pij того, что система не выйдет из состояния Si, а останется в нем.
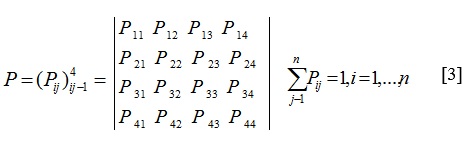
Если, согласно [4], для однородной Марковской цепи заданы начальное распределение вероятностей и матрица переходных вероятностей ||Pij||, то вероятности состояния системы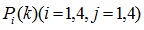 
будут определяться по рекуррентной формуле:
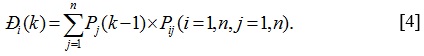
Распишем эту формулу, предположив, что у нас 4 состояния: S1, S2, S3 и S4. Тогда вероятности состояния Pi(k) после первого шага :
Определим вероятности состояний после второго шага:
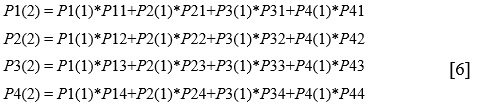
Последовательности состояний функционирования системы ЗИ S(0), S(1)… S(4) – будут рассматриваться как последовательность случайных событий. Вероятность перехода из любого состояния Si в любое Sj не зависит от того, когда и как система пришла в состояние Sj. Начальное состояние S(0) заданно (известно) заранее, путем изучения результатов предыдущих контрольных проверок.
Функционирование системы ЗИ представимо в виде матрицы переходных вероятностей, которая будет иметь вид:
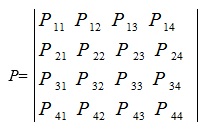
Тогда вероятности состояния системы защиты КТ Р (Si) можно рассчитать по рекуррентной формуле [7]:
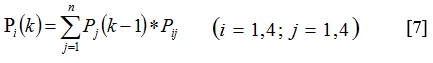
Что позволит определить вероятности нахождения систем защиты коммерческой тайны S в состоянии Sijдля каждого структурного подразделения организации и, в дальнейшем, определить очередность и необходимость контроля их контроля.
